1.前言:
Delta机械臂作为并联机械臂的代表,已广泛的运用于需要精确作业的工业生产之中。不过随着发展,越来越多的工业外的项目也开始采取这种机械臂模式(比如很多无人机上开始装配Delta机械臂进行作业)。本文主要是我在个人学习和应用该机械臂的过程中,顺便写下自己的理解和心得。
2.整体建模:
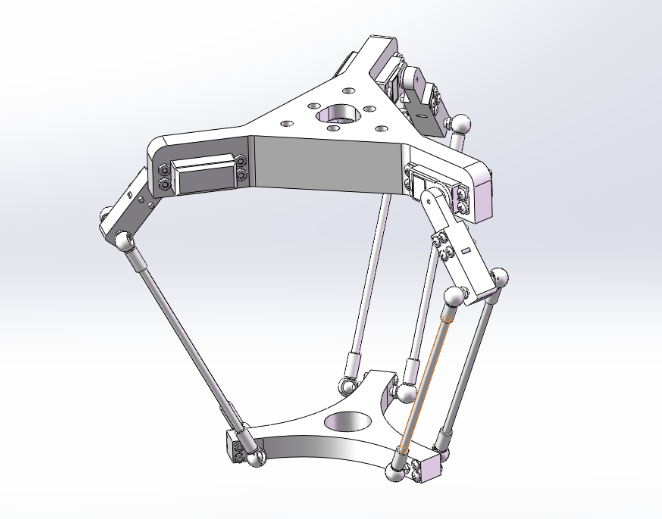
Delta机械臂的实物如上图所示,可以看出,在最上面的是一个静平台(等边三角形),一般在作业中会固定于基座上。连接着静平台的三根杆是三根主动杆,通过他们的转动,来控制下面动平台(同样是个等边三角形)的运动(这里无论主动杆如何摆动,都不会影响下面的动平台面与静平台面保持平行,这算是Delta机械臂的一个特性,具体原理不在此处赘述)。与三根主动杆下端相连的是三根从动杆,其同样与我们的静平台相连。
逆运动学解算的任务大致就是,在知道了末端执行器的目标位置后,通过该目标位置反推出执行机构应该旋转的角度(即通过结果推过程)。

我们首先将整个Delta机械臂建模为上图。R,r分别是动平台和静平台的等边三角形外切圆的半径,C_i(i=1,2,3)为动平台的三个与主动杆相连的端点。原点O 是三角形外切圆的圆心,OC_1是X轴,竖直向上为Z轴,Y轴方向与二者垂直,如图所示。\varphi_i是三个端点顺时针到X轴的角度大小。B_i则是三根主动杆与从动杆的交点,主动杆的长度为L,从动杆的长度为l。A_i为动平台对应着静平台的三个端点。P为静平台外切圆圆心,动平台的坐标系基本是静平台的平移,二者之间只差了一个平移向量。
在这次的逆运动学解算之中,我们主要利用B_iA_i(i = 1,2,3) 的模长不变这一特性,最终通过已知的P点的坐标,来求得每根主动杆应当旋转的角度\theta_i。
3.求解:
首先写出B_i的坐标,B_i = R\left[\begin{array}{ccc} \cos\varphi_i \\ \sin\varphi_i \\ 0 \end{array}\right] + L\left[\begin{array}{ccc} \cos\theta_i\cos\varphi_i \\ \cos\theta_i\sin\varphi_i \\ -\sin\theta_i \end{array}\right],同时由于是逆解运算,我们假设我们已经知道P点的坐标并设为(x,y,z),那么A_i=r\left[\begin{array}{ccc} \cos\varphi_i \\ \sin\varphi_i \\ 0 \end{array}\right]+\left[\begin{array}{ccc} x \\ y \\ z \end{array}\right],我们先前说过我们希望利用的是从动杆的长度不变这一性质,即|\overrightarrow{B_iA_i}| = l。从向量出发,\overrightarrow{B_iA_i}\\=\overrightarrow{OA_i} - \overrightarrow{OB_i}\\=r\left[\begin{array}{ccc} \cos\varphi_i \\ \sin\varphi_i \\ 0 \end{array}\right]+\left[\begin{array}{ccc} x \\ y \\ z \end{array}\right]-R\left[\begin{array}{ccc} \cos\varphi_i \\ \sin\varphi_i \\ 0 \end{array}\right] -L\left[\begin{array}{ccc} \cos\theta_i\cos\varphi_i \\ \cos\theta_i\sin\varphi_i \\ -\sin\theta_i \end{array}\right]。
然后运用一点小技巧,|\overrightarrow{B_iA_i}|^2 = l^2,也即l^2=\\(-r\cos\varphi_i-x+R\cos\varphi_i+L\cos\theta_i\cos\varphi_i)^2 + (r\sin\varphi_i + y - R\sin\varphi_i-L\cos\theta_i\sin\varphi_i)^2+(z+L\sin\theta_i)^2,首先容易观察到,第一个平方项和第二个平方项里面是有可以合并的项的,所以我们先计算前两项的平方和:
=\\((R-r+L\cos\theta_i)\cos\varphi_i-x)^2+((R-r+L\cos\theta_i)\sin\varphi_i-y)^2 =(R-r+L\cos\theta_i)^2+x^2+y^2-2x(R-r+L\cos\theta_i)\cos\varphi_i-2y(R-r+L\cos\theta_i)\sin\varphi_i
接下来我们注意将跟\theta有关的都单独提取出来(别忘了我们整个求解过程中主要找的是谁与谁的关系),所以上面的式子就变成=(R-r)^2+2(R-r)L\cos\theta_i+L^2\cos^2\theta_i+x^2+y^2-2(x\cos\varphi_i+y\sin\varphi)L\cos\theta_i-2(x\cos\varphi_i+y\sin\varphi_i)(R-r)
然后再去求原式:l^2\\=(R-r)^2+2(R-r)L\cos\theta_i+L^2\cos^2\theta_i+x^2+y^2-2(x\cos\varphi_i+y\sin\varphi)L\cos\theta_i-2(x\cos\varphi_i+y\sin\varphi_i)(R-r)+z^2+L^2\sin^2\theta_i+2Lz\sin\theta_i\\=(R-r)^2+L^2+x^2+y^2+z^2-2(x\cos\varphi_i+y\sin\varphi_i)(R-r)+2(R-r-x\cos\varphi_i-y\sin\varphi_i)L\cos\theta_i+2Lz\sin\theta_i 将l^2放到右边,并将已知量化简如下:
那么原式就能够化简如下:
U\cos\theta_i+V\sin\theta_i+M = 0(U,V,M均为已知常数)
然后使用万能公式解方程即可。
\sin\theta_i = \frac{2t}{1+t^2},\cos\theta_i = \frac{1-t^2}{1+t^2},其中t = \tan\frac{\theta_i}{2}
从而,(M-U)t^2+2Vt+(M+U)=0
t = \frac{-V-\sqrt{U^2+V^2-M^2}}{M-U}(U,V,M如上表格所示)
